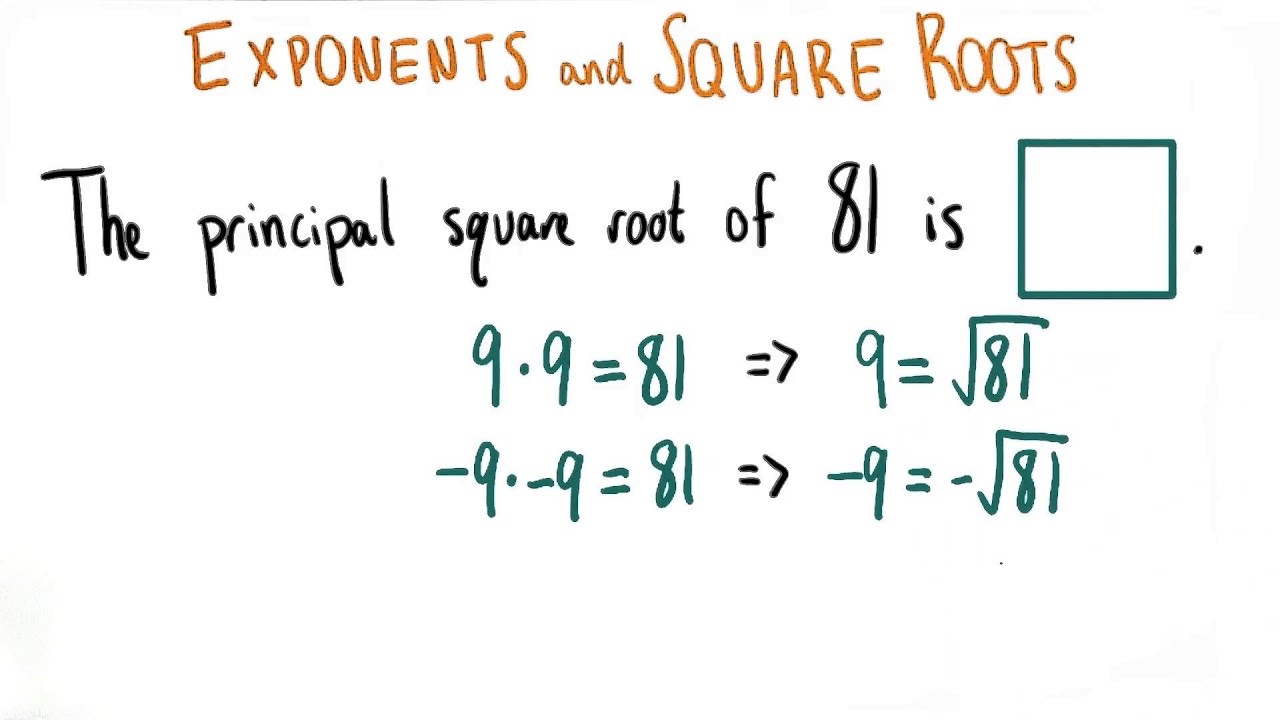The principal square root is a fundamental concept in mathematics that plays a crucial role in various fields, including algebra, geometry, and real-world applications. Understanding the principal square root is vital for students and professionals alike, as it lays the groundwork for more advanced mathematical concepts. In this article, we will explore the definition of the principal square root, its properties, and its significance in practical applications. Whether you are a student looking to grasp this concept or a professional seeking to refresh your knowledge, this article aims to provide a comprehensive overview.
The principal square root of a non-negative number is defined as the non-negative value that, when multiplied by itself, gives the original number. For instance, the principal square root of 9 is 3 since 3 × 3 = 9. This definition is crucial because it highlights the distinction between square roots in general, which can be both positive and negative. Here, we will focus specifically on the principal square root, which is always non-negative.
Throughout this article, we will delve into various aspects of the principal square root, including its mathematical properties, methods for calculation, and its application in solving real-world problems. By the end of this article, you will have a thorough understanding of this essential mathematical concept.
Table of Contents
- Definition of Principal Square Root
- Properties of Principal Square Roots
- How to Calculate Principal Square Roots
- Applications of Principal Square Roots
- Examples of Principal Square Roots
- Common Misconceptions
- Related Concepts in Mathematics
- Conclusion
Definition of Principal Square Root
The principal square root of a number \( x \) is denoted as \( \sqrt{x} \) and is defined as the non-negative number \( y \) such that \( y^2 = x \). For example:
- If \( x = 16 \), then \( \sqrt{16} = 4 \) because \( 4^2 = 16 \).
- If \( x = 0 \), then \( \sqrt{0} = 0 \) since \( 0^2 = 0 \).
- If \( x = 25 \), then \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
It is important to note that while both positive and negative numbers can be square roots of a positive number (e.g., \( 4 \) and \( -4 \) are square roots of \( 16 \)), the principal square root specifically refers only to the non-negative root.
Properties of Principal Square Roots
The principal square root has several important properties that are useful in mathematical calculations:
- Non-Negativity: The principal square root of a non-negative number is always non-negative.
- Identity Property: The principal square root of 0 is 0: \( \sqrt{0} = 0 \).
- Product Property: The principal square root of a product is the product of the principal square roots: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) for non-negative \( a \) and \( b \).
- Quotient Property: The principal square root of a quotient is the quotient of the principal square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for non-negative \( a \) and \( b \) (with \( b \neq 0 \)).
- Power Property: The principal square root of \( a^2 \) is the absolute value of \( a \): \( \sqrt{a^2} = |a| \).
How to Calculate Principal Square Roots
Calculating the principal square root can be done through various methods:
1. Using a Calculator
The simplest way to find the principal square root of a number is to use a scientific calculator. Most calculators have a square root function that allows you to input the number and get the result directly.
2. Estimation
You can estimate the principal square root of a number by identifying two perfect squares between which the number lies. For example, to estimate \( \sqrt{50} \), notice that \( 7^2 = 49 \) and \( 8^2 = 64 \). Thus, \( \sqrt{50} \) is approximately between 7 and 8.
3. Prime Factorization
For perfect squares, you can find the principal square root by using prime factorization. For instance, to find \( \sqrt{36} \), factor \( 36 \) into \( 2^2 \times 3^2 \). The principal square root is \( 2 \times 3 = 6 \).
4. Long Division Method
This method is useful for finding square roots of non-perfect squares and involves a step-by-step division process. It may take longer but can be used for manual calculations.
Applications of Principal Square Roots
The principal square root has numerous applications in various fields:
- Geometry: In geometry, the principal square root is used in calculating the lengths of sides of squares and other geometric shapes.
- Physics: In physics, the principal square root appears in equations involving the Pythagorean theorem and in calculating distances.
- Finance: In finance, the principal square root is used in calculating the standard deviation of data sets, which is crucial for risk assessment.
- Statistics: The principal square root is often used in statistical formulas, including those for variance and correlation.
Examples of Principal Square Roots
To solidify your understanding, let’s explore some examples:
- Find the principal square root of \( 64 \).
Solution: \( \sqrt{64} = 8 \). - Find the principal square root of \( 121 \).
Solution: \( \sqrt{121} = 11 \). - Estimate the principal square root of \( 30 \).
Solution: Between \( 5 \) and \( 6 \) because \( 5^2 = 25 \) and \( 6^2 = 36 \).
Common Misconceptions
Several misconceptions exist regarding the principal square root:
- Misconception: The square root of a negative number is a real number.
Fact: The square root of negative numbers is not defined in the set of real numbers; it leads to complex numbers. - Misconception: All square roots are the same.
Fact: The principal square root is specifically the non-negative root, while the term "square root" can refer to both positive and negative roots.
Related Concepts in Mathematics
Understanding the principal square root leads to the exploration of several related concepts:
- Square Numbers: A square number is the product of an integer multiplied by itself (e.g., \( 1, 4, 9, 16, \) etc.).
- Radicals: Radicals extend the concept of square roots to higher roots (e.g., cube roots) and are represented using the radical symbol.
- Complex Numbers: When dealing with square roots of negative numbers, we enter the realm of complex numbers, which include imaginary units.
Conclusion
In conclusion, the principal square root is a fundamental mathematical concept with a wide range of applications. Understanding its definition, properties, calculation methods, and relevance in various fields is crucial for anyone studying mathematics or working in related professions. We encourage you to practice calculating principal square roots and explore their applications in real-world scenarios.
Feel free to leave your comments or questions below, share this article with others, or check out our other articles for more insights into mathematical concepts!
You Might Also Like
Cougar Paws: The Ultimate Guide To Understanding And Using This Innovative FootwearMonster Hunter: Rise - A Comprehensive Guide To The Thrilling World Of Hunting
Wale Lotus Flower Bomb: The Essence Of Emotion In Music
Exploring The World Of Air Force Lacrosse: A Comprehensive Guide
Kramer Assman: The Rising Star In The Digital World
Article Recommendations
- Tom Hardy A Deep Dive Into The Life And Career Of A Hollywood Icon
- The Untold Story Of The Zach And Jeremy Roloff Feud
- Exploring The Life Of Damon Wayans Jr And His Kids