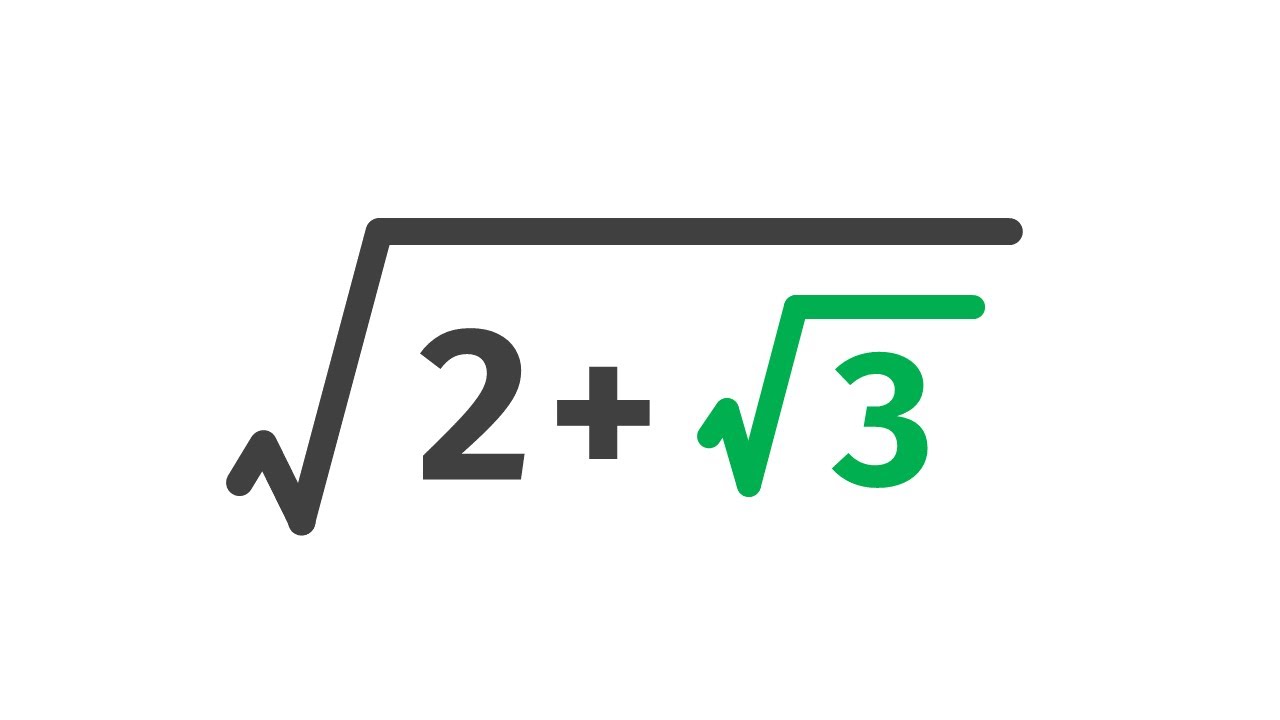The Square Root Of 1: Understanding The Mathematical Concept

The square root of 1 is a fascinating concept in mathematics that often raises questions for learners and enthusiasts alike. Understanding this simple yet intriguing mathematical idea can help in grasping more complex mathematical principles. In this article, we will delve deep into what the square root of 1 signifies, its properties, and its implications in various branches of mathematics.

Not only is the square root of 1 an essential aspect of algebra, but it also plays a role in geometry, calculus, and even practical applications in real life. By exploring this topic, we aim to enhance your mathematical knowledge and provide a solid foundation for further exploration in the world of numbers.

In the following sections, we will break down the square root of 1, examining its definition, properties, and relevance in various mathematical contexts. We will also provide a comprehensive overview that will cater to both beginners and those looking to refresh their knowledge.

Table of Contents

• Definition of Square Root
• Properties of Square Roots
• The Square Root of 1 Explained
• Real-Life Applications of Square Root of 1
• Graphical Representation of Square Root of 1
• Related Mathematical Concepts
• Common Questions about Square Root of 1
• Conclusion

Definition of Square Root

The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, the square root of a number 'x' is denoted as √x.

For instance:

• √4 = 2, because 2 × 2 = 4
• √9 = 3, because 3 × 3 = 9

In this context, we can define the square root of 1 as follows:

• √1 = 1, because 1 × 1 = 1

Properties of Square Roots

Understanding the properties of square roots is essential for solving mathematical problems. Here are some key properties:

• Square roots of non-negative numbers are always non-negative.
• The square root of a product is equal to the product of the square roots: √(a*b) = √a * √b.
• The square root of a quotient is equal to the quotient of the square roots: √(a/b) = √a / √b.
• For any positive number a, √a^2 = a.

The Square Root of 1 Explained

The square root of 1 is unique because it is the only non-negative number whose square is 1. This can be expressed mathematically as:

• √1 = 1
• -√1 = -1

Thus, the square root of 1 has two possible values: 1 and -1. This can be particularly useful in various mathematical contexts, especially when dealing with equations and functions.

Real-Life Applications of Square Root of 1

While the square root of 1 may seem like a trivial concept, it has practical applications in various fields:

• **Physics:** Understanding the relationship between forces and motion often involves the square root function.
• **Finance:** Square roots are used in calculating interest rates and investment growth.
• **Statistics:** The standard deviation formula includes square roots, helping in data analysis.

Graphical Representation of Square Root of 1

Graphically, the square root function can be represented on a coordinate system where the x-axis denotes the input value and the y-axis denotes the output value. The point where x equals 1 will yield y equals 1. This can be visualized as:

• Point (1,1) on the graph of y = √x.

Related Mathematical Concepts

The square root of 1 connects to other mathematical ideas, including:

• **Exponents:** Understanding how square roots relate to fractional exponents (e.g., x^(1/2)).
• **Complex Numbers:** Exploring how roots apply in the context of complex numbers.
• **Quadratic Equations:** Solving equations that may lead to square roots.

Common Questions about Square Root of 1

Here are some frequently asked questions regarding the square root of 1:

• **Q: What is the square root of negative one?**
• A: The square root of negative one is represented as the imaginary unit 'i.'
• **Q: Why is the square root of 1 both 1 and -1?**
• A: Because both values, when squared, yield 1.

Conclusion

In conclusion, the square root of 1 is more than just a simple mathematical concept; it serves as a gateway to understanding more complex mathematical ideas. From its definition and properties to its real-life applications and connections to other mathematical principles, the square root of 1 proves to be an essential topic in mathematics.

We encourage readers to explore further, ask questions, and engage with the fascinating world of mathematics. Feel free to leave comments, share this article, or check out other resources on our site!

Thank you for taking the time to enhance your mathematical knowledge. We hope to see you return for more insightful articles!